从零实现最简编译模型
从零实现最简编译模型
简介
前两日我偶然间在 GitHub 上发现了一个项目:the-super-tiny-compiler,官方介绍说这可能是一个最简的编译器。刚好之前学过「编译原理」这门课,我的兴趣一下子就上来了,简单看了一下,这个项目是将一个 Lisp 表达式转化为 C 的表达式的编译器,中间涉及词法分析、语法分析、AST 树遍历转化以及最后的代码输出环节,下面我就带大家一起来简单实现一下。
词法分析
词法分析也叫解析,每一个编译器需要做的第一步都是词法分析,具体是什么意思呢?简单来说就是把要进行转化的「源代码」拆解开,形成一个一个小部件,称为 token。比如说如下将一个 JavaScript 语句拆解开的例子:
let name = "touryung";
大致分解就可以得到一个 token 数组:[let, name, =, "touryung", ;],这样才有利于进行下一步操作。由于我们此次实现的是最简编译器,因此编译器内部只实现了对小括号、空格、数字、字符串、变量的识别。
整体框架
要实现词法分析器(解析器),首先我们需要先搭出一个框架。词法分析的整体思路就是遍历输入的字符串,然后识别不同的 token,将它保存到 token 数组。
框架如下,不同部分的意思已在注释中标出:
const WHITESPACE = /\s/; // 空格
const NUMBERS = /[0-9]/; // 数字
const LETTERS = /[a-z]/i; // 变量
function tokenizer(input) {
let current = 0; // 当前识别到的下标
let tokens = []; // token 数组
while (current < input.length) {
// 遍历
let char = input[current]; // 当前遍历到的字符
// 不同的 token 识别操作
throw new TypeError(`I dont know what this character is: ${char}`);
}
return tokens;
}
搭出框架,下一步就是识别不同的 token 了。
识别括号
识别括号很简单,当遍历到当前字符是左右括号时,将一个描述当前 token 的对象放入 token 数组即可。
// 识别左括号
if (char === "(") {
tokens.push({ type: "paren", value: "(" }); // 压入描述当前 token 的对象
current++;
continue;
}
// 识别右括号
if (char === ")") {
tokens.push({ type: "paren", value: ")" });
current++;
continue;
}
识别空格
这里需要注意,因为空格实际上对编程语言的语法来说是无关紧要的,这就是为什么将 Javascript 代码压缩之后仍然能够正常运行。因此当我们识别到空格的时候,不需要将其放入 token 数组进行下一步的操作。
实际上,在词法分析这一步,类似空格、注释、换行符这类不影响程序语法的 token 就不会送入下一步进行处理了。
因此,当我们识别到空格的时候,只需要继续遍历即可:
// 空格,不处理
if (WHITESPACE.test(char)) {
current++;
continue;
}
识别数字/变量/字符串
我为什么要把这三种 token 写在一起呢?原因是从数字开始,这三种 token 的匹配逻辑都很相似,由于匹配的 token 可能不再是单个字符,因此需要在内部继续循环直到匹配完整个 token 为止。
// 数字,循环获取数值
if (NUMBERS.test(char)) {
let value = ""; // 匹配的数字赋初值
while (NUMBERS.test(char)) { // 遍历,如果还能匹配就累加
value += char;
char = input[++current];
}
tokens.push({ type: "number", value }); // 压入描述当前 token 的对象
continue;
}
// 变量,和 number 类似
if (LETTERS.test(char)) {
let value = "";
while (LETTERS.test(char)) {
value += char;
char = input[++current];
}
tokens.push({ type: "name", value });
continue;
}
// 字符串,前后的 "" 需要跳过
if (char === '"') {
let value = "";
char = input[++current]; // 跳过前面的引号
while (char !== '"') { // 结束条件,匹配到末尾的引号
value += char;
char = input[++current];
}
char = input[++current]; // 跳过后面的引号
tokens.push({ type: "string", value });
continue;
}
其中需要注意,识别字符串类似上面两种,但是也有两点不同:
- 在字符串识别时需要跳过前后的引号,只匹配中间具体的值;
- 在中间进行遍历的时候结束条件是匹配到末尾的引号。
有人可能会问,如果跳过的前后的引号以后要怎么知道它是字符串呢,这时候压入数组的 token 描述对象作用就出来了,它有一个 type 属性可以指定当前 token 的类型。
小总结
至此,词法分析的工作就做完了,其实相对来说还是很好懂的,那么能不能直观的观察词法分析输出的 token 数组是什么样子的呢?当然可以,只需要编写一个样例测试一下就行了,比如:
let source = "(add 2 (subtract 4 2))"; // 源代码
let tokens = tokenizer(source);
console.log(tokens);
这是一个计算 2+(4-2) 的 Lisp 语句,将它作为输入得到的 token 数组如下所示:
[
{ "type": "paren", "value": "(" },
{ "type": "name", "value": "add" },
{ "type": "number", "value": "2" },
{ "type": "paren", "value": "(" },
{ "type": "name", "value": "subtract" },
{ "type": "number", "value": "4" },
{ "type": "number", "value": "2" },
{ "type": "paren", "value": ")" },
{ "type": "paren", "value": ")" }
]
这样就完美的达到了我们开头所说的将源代码进行拆解的目的。
语法分析
接下来就是语法分析了,语法分析的作用是根据具体的编程语言语法来将上一步输出的 token 数组转化为对应的 AST(抽象语法树),既然涉及到树结构,那么这个步骤自然少不了递归操作。
整体框架
通用的,语法分析部分也需要先搭出一个框架。整体思路就是遍历 token 数组,递归地构建 AST 树,框架如下:
function parser(tokens) {
let current = 0;
function walk() {
let token = tokens[current];
// 将不同的 token 转化为 AST 节点
throw new TypeError(token.type);
}
let ast = {
// 此为 AST 树最外层结构,是固定的
type: "Program",
body: [],
};
while (current < tokens.length) {
// 遍历 token 数组,构建树结构
ast.body.push(walk());
}
return ast;
}
构建数字和字符串节点
这两种节点的构建较为简单,直接返回描述节点的对象即可:
// 构建整数节点
if (token.type === "number") {
current++;
return {
type: "NumberLiteral",
value: token.value,
};
}
// 构建字符串节点
if (token.type === "string") {
current++;
return {
type: "StringLiteral",
value: token.value,
};
}
构建函数调用节点
懂 Lisp 的人都知道,在 Lisp 中括号是精髓,比如函数调用类似于这种形式: (add 1 2)。因此我们需要以括号来进行识别,具体的代码如下:
if (token.type === "paren" && token.value === "(") {
// 左括号开始
token = tokens[++current]; // 跳过左括号
let node = {
// 函数调用节点
type: "CallExpression",
name: token.value,
params: [],
};
token = tokens[++current]; // 跳过 name
// 只要不是右括号,就递归收集参数节点
while (!(token.type === "paren" && token.value === ")")) {
node.params.push(walk()); // 添加参数
token = tokens[current];
}
current++; // 跳过右括号
return node;
}
这里面需要注意的点是,某一个参数也可能是函数调用的结果,因此在解析参数时需要递归调用 walk 函数。
还有另外一点值得一提,那就是我们多次用到了这种代码结构:
if (value === "(") {
// ...
while (!value === ")") {
// ...
}
}
很明显,这种结构就是适用于遍历某个区间,因此我们在分析字符串、括号这种配对元素时就需要使用这种结构。
小总结
就进行这样简单的几个步骤,前面的 token 数组就会被我们转化成 AST 树结构了,感觉还是非常的神奇,此时,我们的输出以及编程了如下这样:
{
"type": "Program",
"body": [
{
"type": "CallExpression",
"name": "add",
"params": [
{
"type": "NumberLiteral",
"value": "2"
},
{
"type": "CallExpression",
"name": "subtract",
"params": [
{
"type": "NumberLiteral",
"value": "4"
},
{
"type": "NumberLiteral",
"value": "2"
}
]
}
]
}
]
}
遍历并转化 AST 树
此时我们已经得到了一棵 AST 树,编译器之所以能够将源代码转化为目标代码实际上就可以视作将源 AST 树转化为目标 AST 树,要实现这种转化过程,我们就需要对树进行遍历,然后对对应的节点进行操作。
遍历树
我们从上面可以看出,AST 树中的 body 属性和函数调用的参数实际上都是数组类型的,因此我们首先需要定义对数组类型的遍历方法,很简单,只需要遍历数组中的每个元素分别进行遍历就行了:
// 访问(参数)数组
function traverseArray(array, parent) {
array.forEach((child) => traverseNode(child, parent));
}
当遍历到具体的节点时,我们就需要调用此节点类型的 enter 方法来进行访问(转化 AST)操作,不同类型的节点 enter 方法是不一样的。
function traverseNode(node, parent) {
let method = visitor[node.type]; // 去除当前类型的方法
if (method && method.enter) {
// 执行对应 enter 方法
method.enter(node, parent);
}
switch (
node.type // 对不同类型节点执行不同的遍历操作
) {
case "Program":
traverseArray(node.body, node);
break;
case "CallExpression":
traverseArray(node.params, node);
break;
case "NumberLiteral":
case "StringLiteral":
break;
default:
throw new TypeError(node.type);
}
}
可能有人又要问,为什么执行 enter 方法时第二个参数需要传入父节点呢?这其实和后面的实际转化部分的逻辑相关,我们就放到后面来进行解释。
转化 AST 树
整体框架
一样的,我们可以首先搭出大体的框架,具体的同类型的节点访问(转化)方法后面再说。这里的转化思路就比较重要了:我们要如何在遍历旧的 AST 树时能将转化后的节点加入新的 AST 树?
这里的实现思路大体分为以下几步:
- 在旧的 AST 树中加入一个
_context上下文属性,指向新的 AST 树的数组节点 - 当遍历旧 AST 数组节点的子元素时,将转化后的子元素放入它的父元素的
_context属性中 - 根据 JavaScript 引用类型的特点,此时就实现了将转化和的节点放入新 AST 树的目的。
在图中表示出来大概如下:
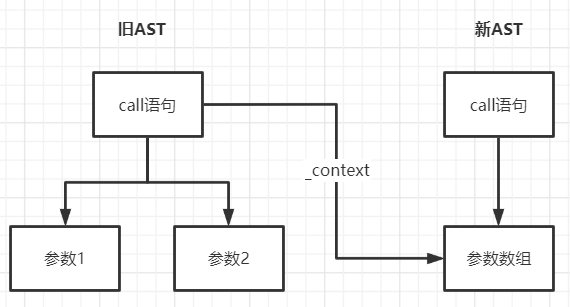
我相信这已经回答了上面执行 enter 方法时为什么第二个参数需要传入父节点的问题。
function transformer(ast) {
let newAst = {
// 新 AST 树的最外层结构
type: "Program",
body: [],
};
// _context 用于遍历旧子节点时压入新 ast
ast._context = newAst.body;
let visitor = {
// 不同类型的节点访问(转化)方法
};
traverser(ast, visitor); // 开始遍历旧 AST 树
return newAst;
}
数字和字符串的转化
{
NumberLiteral: {
enter(node, parent) {
parent._context.push({ // 压入新 AST 树
type: "NumberLiteral",
value: node.value,
});
},
},
StringLiteral: {
enter(node, parent) {
parent._context.push({
type: "StringLiteral",
value: node.value,
});
},
}
}
函数调用节点的转化
函数调用节点特殊一点,由于它的参数可以视作它的子节点,因此需要将当前节点的 _context 属性指向新 AST 树对应的参数数组。
还有一点特殊的是,如果当前的函数调用不是嵌套在别的函数调用中,那么就可以再加一个 ExpressionStatement 信息,表示当前节点是一整个语句,比如 (add 2 (subtract 4 2)) 内层的括号就不能称作一个完整的语句,因为它是作为另一个函数的参数形式存在的。
{
CallExpression: {
enter(node, parent) {
let expression = { // 新 AST 树的函数调用节点
type: "CallExpression",
callee: {
type: "Identifier",
name: node.name,
},
arguments: [],
};
node._context = expression.arguments; // 参数数组处理
// 如果当前的函数调用不是嵌套在别的函数调用中
if (parent.type !== "CallExpression") {
expression = {
type: "ExpressionStatement",
expression: expression,
};
}
parent._context.push(expression);
},
},
}
小总结
截至目前,我们已经完成了 AST 树的遍历和转化工作,这部分的工作量不小,但是也是整个编译中最精华的部分,如果顺利的话,我们现在可以得到如下转化后的新 AST 树:
{
"type": "Program",
"body": [
{
"type": "ExpressionStatement",
"expression": {
"type": "CallExpression",
"callee": {
"type": "Identifier",
"name": "add"
},
"arguments": [
{
"type": "NumberLiteral",
"value": "2"
},
{
"type": "CallExpression",
"callee": {
"type": "Identifier",
"name": "subtract"
},
"arguments": [
{
"type": "NumberLiteral",
"value": "4"
},
{
"type": "NumberLiteral",
"value": "2"
}
]
}
]
}
}
]
}
这就是对应 C 代码的 AST 树的结构了,将它与之前 Lisp 的 AST 树相比,还是可以看出很多不同的。
代码生成
最后,就是最激动人心的时刻了,生成目标代码!这一步相对轻松,根据上一步生成的 AST 树,对它进行递归遍历并生成最终的代码:
function codeGenerator(node) {
switch (node.type) {
case "Program":
return node.body.map(codeGenerator).join("\n");
case "ExpressionStatement":
return `${codeGenerator(node.expression)};`;
case "CallExpression": // 生成函数调用式
return `${codeGenerator(node.callee)}(${node.arguments
.map(codeGenerator)
.join(", ")})`;
case "Identifier": // 生成变量名
return node.name;
case "NumberLiteral":
return node.value; // 生成数字
case "StringLiteral":
return `"${node.value}"`; // 生成字符串(别忘了两边的引号)
default:
throw new TypeError(node.type);
}
}
最终,我们实现了从 Lisp 的示例代码 (add 2 (subtract 4 2)) 到 C 语言代码 add(2, subtract(4, 2)) 的转化。
大总结
本篇文章带大家从零实现了一个编译器最基本的功能,涉及了词法分析、语法分析、AST 树遍历转化等内容。编译原理听似高深(确实高深),但是基础的部分就是那些内容,啥词法分析语法分析的,最终都会回归到对字符串的处理。
我研究的方向是前端,那别人可能认为平时可能都不会涉及到编译原理的内容,但是实际上一旦深入研究的话,类似 Babel 将 ES6+ 的代码转化为 ES5 之类的工作实际上都是编译器做的工作,还有最近很火的 esbuild,只要涉及到代码的转化,肯定都会涉及编译,甚至 Vue 内部也有一个编译器用于模板编译。
说了这么多,本意还是希望大家在平时的学习中要多多涉猎新领域的知识,扩展自己的技能面,这样才能提高自己的技术视野和上限。
最后,推荐一个我最近在学习的最简 Vue 模型项目,也可以在这里面学习到 Vue 中模板编译的原理。
(全文终)